강화학습_week3 (Bellman Equation)

이번에는 Bellman Equation에 대해서 정리!!!

1. Bellman Equation이란?

🔸 핵심 정의

Bellman Equation(벨만 방정식)은 어떤 상태 또는 행동의 가치(value)를 “지금 받는 보상 + 미래 가치” 로 나누어 재귀적으로 정의한 수식입니다.

🔍 이게 왜 중요한가?

강화학습에서는 우리가 알고 싶은 게 딱 하나입니다:

“지금 어떤 상태(또는 행동)가 얼마나 좋은가?”
(즉, 이걸 하면 얼마나 좋은 결과가 따를까?)

그런데 이 질문에 직접 답하기는 어렵습니다.
→ 그래서 이 가치를 계산하기 위해 미래에 일어날 일을 예측해서 추론합니다.
→ 이 때 사용하는 수식이 바로 Bellman Equation입니다.

 

2. Bellman Expectation Equation (기댓값 버전)

▶ 상태 가치 함수 Vπ(s)

즉,

상태 s에서 시작했을 때,
정책 π를 따르며 받게 될 총 보상의 기대값

좀 더 풀어 쓰면:

▶ 행동 가치 함수 Qπ(s,a)

→ 이 수식은 상태-행동 쌍의 가치를 평가합니다.

 

3. 역할: MDP에서 Bellman Equation이 왜 중요한가?

✅ 1) 정책 평가 (Policy Evaluation)

• 주어진 정책 ππ가 얼마나 좋은지를 평가할 수 있음
• Bellman Equation을 기반으로 반복 계산(iteration) 하면서 Vπ(s)Vπ(s) 또는 Qπ(s,a)Qπ(s,a) 를 추정

---

✅ 2) 정책 개선 (Policy Improvement)

• 계산된 Qπ(s,a)Qπ(s,a)를 바탕으로 더 나은 행동을 선택 → 새로운 정책 π′π′
• 반복하면 결국 최적 정책 π∗π∗ 로 수렴

---

✅ 3) 최적 정책 구하기 (Optimal Policy via Bellman Optimality Equation)

Bellman Optimality Equation은 다음과 같습니다:

▶ 상태 가치 함수 기준:

▶ 행동 가치 함수 기준:

📌 여기서 핵심은:

최적 정책은 Q∗Q∗ 값을 최대화하는 행동을 선택하면 된다.

 

---

🔧 4. 행렬 형태로 표현 (작은 문제일 때만 사용 가능)

Bellman Equation은 행렬 형태로도 표현 가능합니다:

• V: 모든 상태의 가치 벡터
• R: 보상 벡터
• P: 전이 확률 행렬
• I: 단위 행렬

직접 해를 구하려면:

하지만 큰 문제에서는 비현실적이므로 다음과 같은 반복법 사용:

• Dynamic Programming (정책 반복, 가치 반복)
• Monte Carlo Evaluation
• Temporal Difference Learning (TD)

---

📌 마무리 요약

 

---

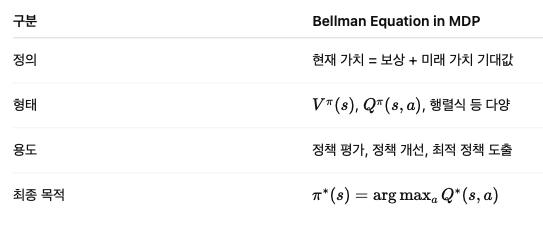
✅ 한 줄 요약

Bellman Equation은 MDP에서 가치 함수의 구조를 수식으로 나타낸 핵심 공식이며,
정책을 평가하고 최적화하는 모든 강화학습 알고리즘의 기초가 됩니다.